棋盘落子位置检测,蒙特卡洛搜索及强化学习,人工智能课程大作业,人为设定函数的alpha-beta剪枝没来得及做,有点离谱。
概述:
主要分为棋盘检测和五子棋AI实现两部分,棋盘检测首先利用opencv进行图像处理,分割为单个棋盘格,再通过CNN对单个棋盘格图片进行分类,得到棋子类别。五子棋AI实现分别用纯蒙特卡洛方法和基于AlphaZero的简化方法实现。
环境:
python==3.7.4
numpy==1.19.4
torch==1.7.1
实现:
棋盘检测image_process.py:
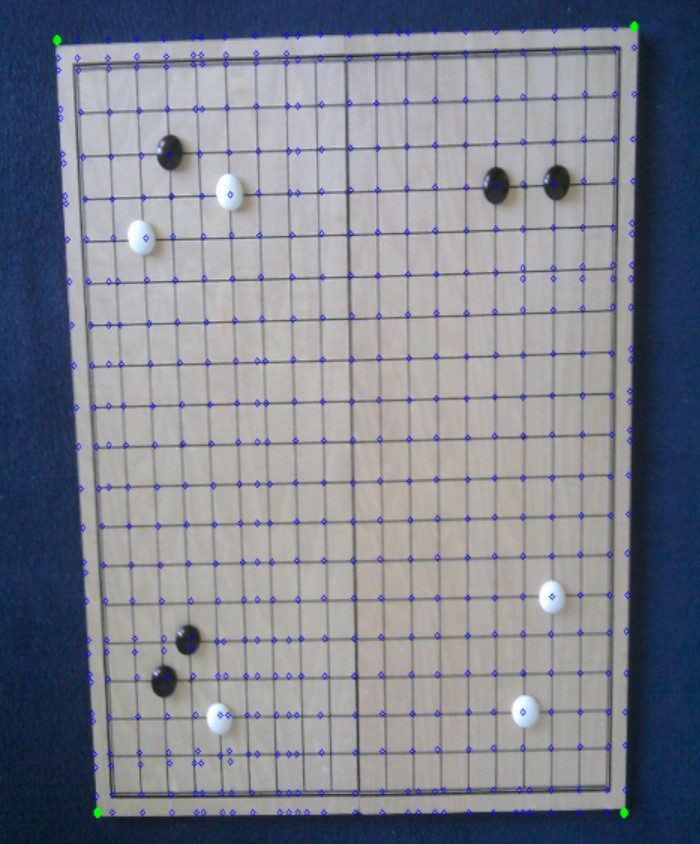
由于可用的训练数据较少, 棋盘检测采取先分割再检测的方法,将棋盘图片分割为单个棋盘格,再对每个棋盘格利用监督学习方法分类为空格、黑棋和白棋。
1.棋盘位置检测:
棋盘检测流程为:
- canny边缘检测
- hough直线检测
- 直线交点聚类得到棋盘角
- 棋盘矫正和分割
canny:
hough:
def hough_lines(img):
rho, theta, threshold = 2, np.pi/180, 250
lines = cv2.HoughLines(img,rho,theta,threshold)
return lines
聚类直线交点:
def cluster_intersections(points, max_dist=5):
Y = spatial.distance.pdist(points)
Z = clstr.hierarchy.single(Y)
T = clstr.hierarchy.fcluster(Z, max_dist, 'distance')
clusters = defaultdict(list)
for i in range(len(T)):
clusters[T[i]].append(points[i])
clusters = clusters.values()
clusters = map(lambda arr: (np.mean(np.array(arr)[:, 0]), np.mean(np.array(arr)[:, 1])), clusters)
result = []
for point in clusters:
result.append([point[0], point[1]])
return result
取四个角:
图像变换:

分割后得到19*19幅图片,单个图片如下:



此方法受棋盘拍摄角度影响小,可以较好处理如下图的情况
处理后:
对图进行标记,并旋转、翻转来扩展训练集,得到黑、白、空图片分别约300、400、2000张,按 8:1:1 分到 train/val/test文件夹
2.监督学习识别棋子net.py
CNN结构:
class ChessNet(nn.Module):
def __init__(self):
super(ChessNet, self).__init__()
# Defining the convolutional layers of the net
self.conv1 = nn.Conv2d(3, 8, kernel_size=5)
self.conv2 = nn.Conv2d(8, 20, kernel_size=5)
self.conv3 = nn.Conv2d(20, 50, kernel_size=5)
self.dropout1 = nn.Dropout()
self.dropout2 = nn.Dropout()
# Defining the fully connected layers of the net
self.fc1 = nn.Linear(4 * 4 * 50, 64)
self.fc2 = nn.Linear(64, 32)
self.fc3 = nn.Linear(32, 3)
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, 2)
x = F.relu(self.conv2(x))
x = self.dropout1(x)
x = F.max_pool2d(x, 2)
x = F.relu(self.conv3(x))
x = self.dropout2(x)
x = F.max_pool2d(x, 2)
x = x.view(-1, 4 * 4 * 50) # Convert 2d data to 1d
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
数据集数据规整,训练结果较好:

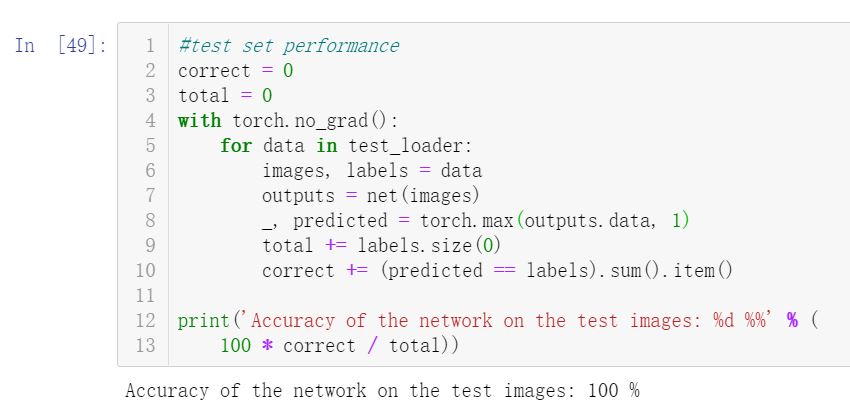
test set:
显示几张test set 中图片及其网络对应输出(E-空, W-白, B-黑):


ChessAI
传统方法通过搜索博弈树和搜索过程中alpha-beta剪枝来实现,人工设置对局势的评估函数。
α值:有或后继的节点,取当前子节点中的最大倒推值为其下界 β值:有与后继的节点,取当前子节点中的最小倒推值为其上界
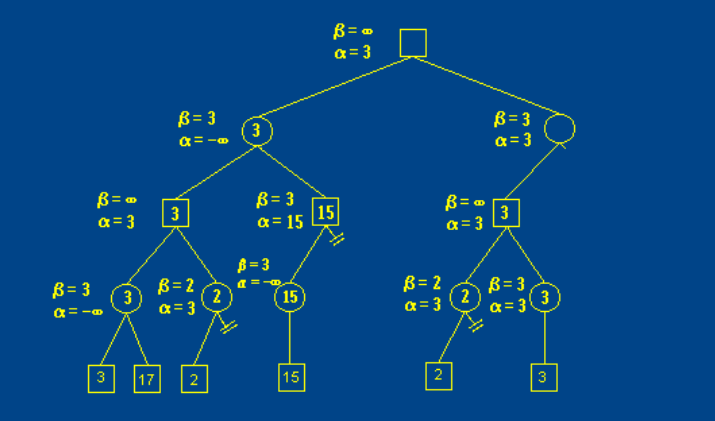
对于不满足α<=N<=β的节点剪枝, 到达搜索深度后即评估局势并返回值
为了方便后续神经网络的应用,此处直接使用纯蒙特卡洛方法
游戏状态表示及棋盘显示界面
**1. 游戏显示
运行游戏: main.py
设置模式:
# play mode
USER_VS_USER_MODE = 0
USER_VS_AI_MODE = 1
AI_VS_AI_MODE = 2
GAME_PLAY_MODE = 1
玩家:
class MAP_ENTRY_TYPE(IntEnum):
MAP_EMPTY = 0,
MAP_PLAYER_ONE = 1,
MAP_PLAYER_TWO = 2
显示界面方法定义在 GameMap.py中, map[][]记录棋盘,可通过更改 CHESS_LEN改变棋盘大小
2.游戏状态
游戏状态类定义在 GameState.py,记录棋盘board、前一步x,y、当前玩家turn:
def __init__(self, board, x, y, turn):
self.board = board
self.x = x
self.y = y
self.result = None
self.turn = turn
if self.turn == MAP_ENTRY_TYPE.MAP_PLAYER_ONE:
self.next_to_move = MAP_ENTRY_TYPE.MAP_PLAYER_TWO
else:
self.next_to_move = MAP_ENTRY_TYPE.MAP_PLAYER_ONE
game_result()返回游戏结果,函数判断前一步落子点(self.x, self.y)四个方向直线上的9个棋子是否构成5连
def game_result(self):
"""
return:
1 if player #1 wins
-1 if player #2 wins
0 if there is a draw
None if result is unknown
"""
dir_offset = [(1, 0), (0, 1), (1, 1), (1, -1)] # direction
line = np.zeros(9)
for i in range(4): # dir
chess_range = 0
for k in range(-4, 5): # count 9 position
dx = self.x + k * dir_offset[i][0]
dy = self.y + k * dir_offset[i][1]
if CHESS_LEN > dx >= 0 and CHESS_LEN > dy >= 0:
line[k+4] = self.board[dy][dx]
else:
line[k+4] = 0
move(action)返回执行action后的下个状态GameState
def move(self, action):
"""
consumes action
return:
GameState
"""
new_board = copy.deepcopy(self.board)
new_board[action.y][action.x] = self.next_to_move.value
return GameState(new_board, action.x, action.y, action.turn)
get_valid_moves()返回可用action的list
def get_valid_moves(self):
"""
returns list of legal action at current game state
Returns
list of GameAction
"""
indices = np.where(self.board.T == 0)
return [
ChessMove(coords[0], coords[1], self.next_to_move)
for coords in list(zip(indices[0], indices[1]))
]
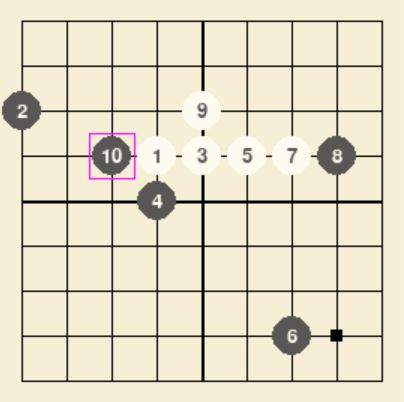
纯蒙特卡洛方法
蒙特卡洛搜索分为三个阶段:
- Select
- Expand
- Backup
每个节点需记录:
Q , 计算为子节点win - lose
N,访问次数
对于未扩展过的节点进行扩展,对于已扩展的节点,选择高UCT的子节点,到达未访问节点后rollout,纯蒙特卡洛方法采用随机方式rollout,直到到达终止状态,将结果反传并更新路径中节点的Q、V。
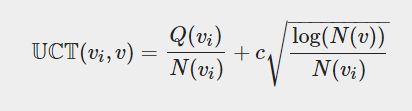
实现:
树节点类class MonteCarloTreeSearchNode()
每个节点保存当前状态state, 访问次数等, 主要成员函数如下:
def q(self):
wins = self._results[self.parent.state.next_to_move]
loses = self._results[-1 * self.parent.state.next_to_move]
return wins - loses
def n(self):
return self._number_of_visits
def expand(self):
action = self.untried_actions.pop()
next_state = self.state.move(action)
child_node = TwoPlayersGameMonteCarloTreeSearchNode(
next_state, parent=self
)
self.children.append(child_node)
return child_node
def is_terminal_node(self):
return self.state.is_game_over()
def rollout(self):
current_rollout_state = self.state
while not current_rollout_state.is_game_over():
possible_moves = current_rollout_state.get_legal_actions()
action = self.rollout_policy(possible_moves)
current_rollout_state = current_rollout_state.move(action)
print("rollout:\n")
print(current_rollout_state.board)
return current_rollout_state.game_result()
def backpropagate(self, result):
self._number_of_visits += 1.
self._results[result] += 1.
if self.parent:
self.parent.backpropagate(result)
def best_child(self, c_param=1.4):
choices_weights = [
(c.q / c.n) + c_param * np.sqrt((2 * np.log(self.n) / c.n))
for c in self.children
]
return self.children[np.argmax(choices_weights)]
def rollout_policy(self, possible_moves):
return possible_moves[np.random.randint(len(possible_moves))]
TreeSearch.py:
调用函数beat_action() 进行simulations_number次蒙特卡洛搜索并返回最优策略
class MonteCarloTreeSearch(object):
def __init__(self, board, x, y, turn):
"""
node : mctspy.tree.nodes.MonteCarloTreeSearchNode
"""
node = TwoPlayersGameMonteCarloTreeSearchNode(GameState(board, x, y, turn))
self.root = node
def best_action(self, simulations_number):
for _ in range(0, simulations_number):
v = self._tree_policy()
print("select:\n")
print(v.state.board)
reward = v.rollout()
print("result:")
print(reward)
v.backpropagate(reward)
return self.root.best_child(c_param=0.)
def _tree_policy(self):
"""
selects node to run rollout/playout for
"""
current_node = self.root
while not current_node.is_terminal_node():
if not current_node.is_fully_expanded():
return current_node.expand()
else:
current_node = current_node.best_child()
return current_node
结果:
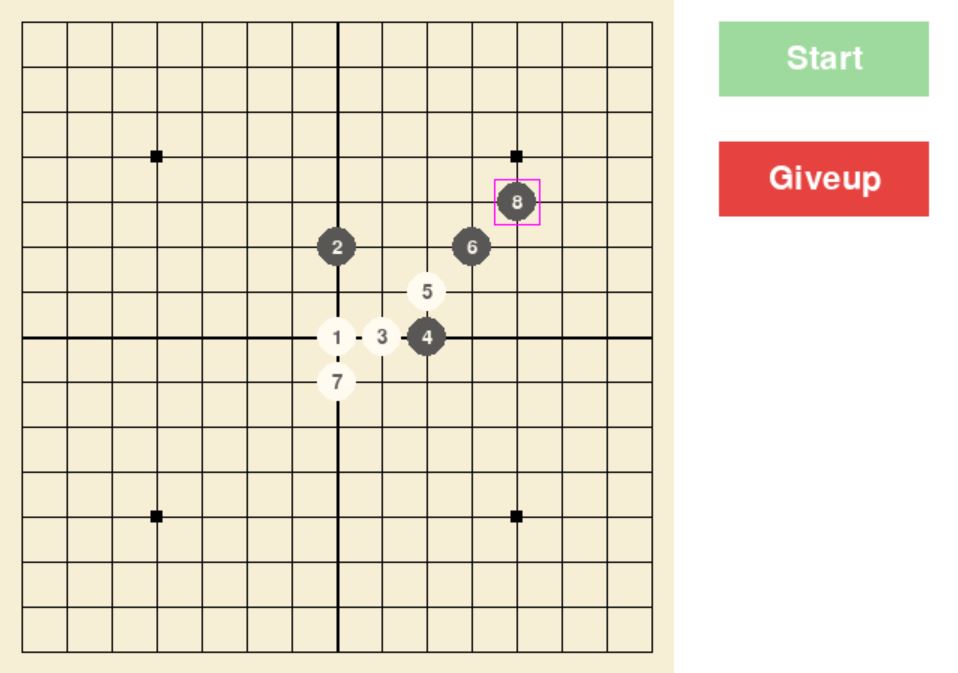
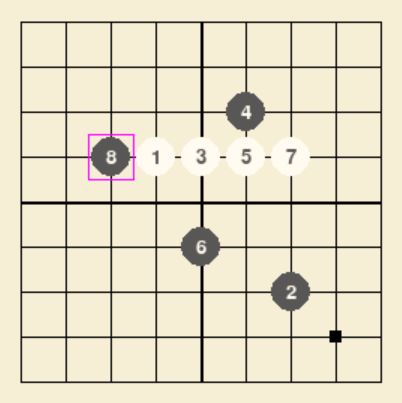
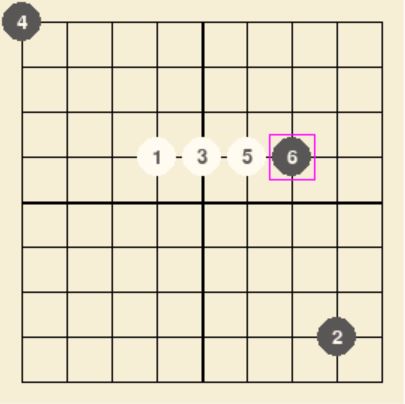
9*9棋盘
SIMULATION_NUM=1000:
SIMULATION_NUM=2000:
能堵四连的情况,但棋力较弱,且计算时间较长。
结合神经网络
基于AlphaZero的结构, 将mcts与policy-value network结合, 通过自我对弈进行强化学习
在rollout阶段不采用随机方式,而是利用神经网络, 神经网络输入棋盘状态s,输出policy和value,指导mcts的选择,mcts模拟的结果(节点状态,概率,结果)作为训练数据训练网络,不断学习。
网络损失函数: $$ l = \sum_t (v_\theta(s_t) - z_t)^2 - \vec{\pi}_t \cdot \log(\vec{p}_\theta(s_t)) $$
训练样本: $$ (s_t, \vec{\pi}_t, z_t) $$
改变上述节点结构,见MonteCarlo.py中class Node
存储节点的先验概率:
class Node:
def __init__(self, prior, game_state):
self.visit_count = 0
self.to_play = game_state.turn
self.prior = prior
self.value_sum = 0
self.children = []
self.game_state = game_state
计算UCB: $$ U(s,a) = Q(s,a) + c_{puct}\cdot P(s,a)\cdot\frac{\sqrt{\Sigma_b N(s,b)}}{1+N(s,a)} $$
def ucb_score(parent, child):
prior_score = child.prior * math.sqrt(parent.visit_count) / (child.visit_count + 1)
if child.visit_count > 0:
# The value of the child is from the perspective of the opposing player
value_score = -child.value()
else:
value_score = 0
return value_score + prior_score
模拟后选择下一步移动的策略: $$ \vec{\pi}(s) = N(s, \cdot)^{1/\tau}/\sum_b(N(s,b)^{1/\tau}) $$
def select_action(self, temperature):
"""
Select action according to the visit count distribution and the temperature.
"""
visit_counts = np.array([child.visit_count for child in self.children])
actions = [child.game_state.action for child in self.children]
if temperature == 0:
action = actions[np.argmax(visit_counts)]
elif temperature == float("inf"):
action = np.random.choice(actions)
else:
visit_count_distribution = visit_counts ** (1 / temperature)
visit_count_distribution = visit_count_distribution / sum(visit_count_distribution)
action = np.random.choice(actions, p=visit_count_distribution)
return action
选择子节点时选择最高ucb值子节点:
def select_child(self):
"""
Select the child with the highest UCB score.
"""
best_score = -np.inf
best_action = -1
best_child = None
for child in self.children:
score = ucb_score(self, child)
if score > best_score:
best_score = score
best_action = child.game_state.action
best_child = child
return best_action, best_child
扩展节点,存在Node的children[]中:
def expand(self, game_state, valid_moves, action_probs):
"""
Expand a node and keep track of the prior policy probability given by neural network
"""
self.game_state = game_state
for a, prob in enumerate(action_probs):
self.children.append(Node(prior=prob, game_state=game_state.move(valid_moves[a])))
类MCTS 见MonteCarlo.py:
参数包含状态、网络模型
class MCTS:
def __init__(self, game_state, model):
self.game_state = game_state
self.model = model
self.state = game_state.state
主要的运行函数, 根据网络对当前棋盘状态模拟SIMULATION_NUM次,并返回根节点:
def run(self):
root = Node(0, self.game_state)
# EXPAND root
action_probs, value = self.model.policy_value_fn(self.game_state)
valid_moves_flatten = self.game_state.valid_moves_flatten()
valid_moves = self.game_state.get_valid_moves()
action_probs = action_probs[np.argwhere(valid_moves_flatten).flatten()] # remove invalid moves
action_probs /= np.sum(action_probs)
root.expand(self.game_state, valid_moves, action_probs)
for _ in range(SIMULATION_NUM):
node = root
search_path = [node]
# SELECT
while node.expanded():
action, node = node.select_child()
search_path.append(node)
parent = search_path[-2]
next_game_state = node.game_state
# The value of the new state from the perspective of the other player
value = next_game_state.game_result()
if value is None:
# If the game has not ended:
# EXPAND
action_probs, value = self.model.policy_value_fn(next_game_state)
valid_moves = next_game_state.get_valid_moves()
valid_moves_flatten = next_game_state.valid_moves_flatten()
action_probs = action_probs[np.argwhere(valid_moves_flatten).flatten()] # remove invalid moves
action_probs /= np.sum(action_probs)
node.expand(next_game_state, valid_moves, action_probs)
self.backpropagate(search_path, value, parent.game_state.next_to_move * -1)
return root
下一步通过自我博弈来生成训练数据,见SelfPlay.py
不断根据现有模型生成下一步策略直至一方胜出,记录每一步的棋局状态state[], 模拟中的概率分布(子节点访问次数比)mcts_prob[],一方胜出后即得到了对应每个状态的z(对于双方玩家z值相反)
def self_play_data(model):
states, mcts_probs, current_players = [], [], []
current_player = MAP_ENTRY_TYPE.MAP_PLAYER_ONE
board = np.zeros((CHESS_LEN, CHESS_LEN))
game_state = GameState(board, 0, 0, -1)
while True:
states.append(game_state.current_state())
current_players.append(game_state.turn)
mcts = MCTS(game_state, model)
root = mcts.run()
action_probs = [0 for _ in range(CHESS_LEN*CHESS_LEN)]
for child in root.children:
act = child.game_state.action
action_probs[act.x*CHESS_LEN+act.y] = child.visit_count
action_probs = action_probs / np.sum(action_probs)
mcts_probs.append(action_probs)
action = root.select_action(temperature=0)
game_state = game_state.move(action)
# print(game_state.board)
reward = game_state.game_result()
if reward is not None:
winners_z = np.zeros(len(current_players))
if reward != 0:
winners_z[np.array(current_players) == reward] = 1.0
winners_z[np.array(current_players) != reward] = -1.0
return reward, zip(states, mcts_probs, winners_z)
policy-value网络
能力有限,时间紧张,网络直接使用了 https://github.com/junxiaosong/AlphaZero_Gomoku 的网络结构。
棋局表示使用了4个8*8的二值特征平面,前两个平面分别表示当前玩家的棋子位置和对手player的棋子位置,第三个平面表示最近一步的落子位置,第四个平面表示的是当前player是不是先手player,如果是先手player则整个平面全部为1,否则全部为0。
def current_state(self):
"""
the board state from the perspective of the current player.
state shape: 4*width*height
"""
mat = self.board.T
square_state = np.zeros((4, CHESS_LEN, CHESS_LEN))
square_state[0][mat == self.turn] = 1.0
square_state[1][mat == self.next_to_move] = 1.0
# indicate the last move location
square_state[2][self.x, self.y] = 1.0
if self.turn == MAP_ENTRY_TYPE.MAP_PLAYER_ONE:
square_state[3][:, :] = 1.0
return square_state[:, ::-1, :]
3层公共全卷积网络,使用ReLu激活函数。然后再分成policy和value两个输出,policy端用11的filter进行降维,再接一个全连接层,使用softmax非线性函数直接输出棋盘上每个位置的落子概率;value端用2个1*1的filter进行降维,再接一个64个神经元的全连接层,最后再接一个全连接层,使用tanh非线性函数直接输出[-1,1]之间的局面评分。
class Net(nn.Module):
"""policy-value network module"""
def __init__(self, board_width, board_height):
super(Net, self).__init__()
self.board_width = board_width
self.board_height = board_height
# common layers
self.conv1 = nn.Conv2d(4, 32, kernel_size=3, padding=1)
self.conv2 = nn.Conv2d(32, 64, kernel_size=3, padding=1)
self.conv3 = nn.Conv2d(64, 128, kernel_size=3, padding=1)
# action policy layers
self.act_conv1 = nn.Conv2d(128, 4, kernel_size=1)
self.act_fc1 = nn.Linear(4*board_width*board_height,
board_width*board_height)
# state value layers
self.val_conv1 = nn.Conv2d(128, 2, kernel_size=1)
self.val_fc1 = nn.Linear(2*board_width*board_height, 64)
self.val_fc2 = nn.Linear(64, 1)
def forward(self, state_input):
# common layers
x = F.relu(self.conv1(state_input))
x = F.relu(self.conv2(x))
x = F.relu(self.conv3(x))
# action policy layers
x_act = F.relu(self.act_conv1(x))
x_act = x_act.view(-1, 4*self.board_width*self.board_height)
x_act = F.log_softmax(self.act_fc1(x_act))
# state value layers
x_val = F.relu(self.val_conv1(x))
x_val = x_val.view(-1, 2*self.board_width*self.board_height)
x_val = F.relu(self.val_fc1(x_val))
x_val = F.tanh(self.val_fc2(x_val))
return x_act, x_val
在训练过程中,保存当前最新模型,self-play数据直接由当前最新模型生成,并用于训练更新自身。但由于计算资源受限,训练速度较慢,8*8棋盘每步模拟400次,经过100局对弈loss从4.8降至3.2左右
batch i:101, episode_len:23
kl:0.00891,lr_multiplier:0.667,loss:3.3900258541107178,entropy:3.2891287803649902,explained_var_old:0.853,explained_var_new:0.874
batch i:102, episode_len:31
kl:0.02935,lr_multiplier:0.667,loss:3.3679325580596924,entropy:3.244642496109009,explained_var_old:0.844,explained_var_new:0.876
batch i:103, episode_len:41
kl:0.03244,lr_multiplier:0.667,loss:3.3015928268432617,entropy:3.254746198654175,explained_var_old:0.883,explained_var_new:0.906
本程序中直接使用了现有模型best_policy.model
分析
由于可用棋盘照片数据少,采用了分割后再检测的方式,棋盘检测算法对于单个棋子的检测效果好,但同时检测结果受到图像分割情况的影响较大,虽然对当前数据集图像分割效果好,对于不同光照条件的棋盘,图像分割的参数可能需要不断调整。
AI方面,纯蒙特卡洛方法需要较多次数的模拟,运用强化学习方法后,通过自我对弈,AI的水平不断提高,可以得到较好的效果。