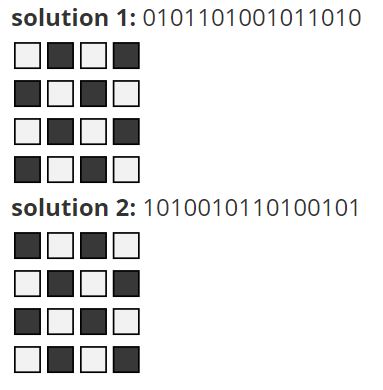
Nonogram Solver 1

​

Nonograms是一种逻辑性图片益智游戏，玩家根据网格旁的数字，将网格中的方格填色或留空，从而展现一副隐藏的图画。本文详细描述了Nonogram求解的方法。

这些数字通过离散断层方式来计算有多少条完整的线会被填入到横向或纵向的方格中。例如，“4 8 3”表示按顺序分别有4个、8个和3个连续方格要填色，且各组填色方格之间至少有一个留空方格。

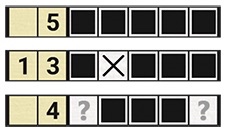
要解开一个图谜，玩家要决定哪些方格需要填色，哪些方格需要留空。

实现功能：

• 从图像文件生成游戏
• 根据文件内游戏提示求解

博客分为两篇， 本篇介绍求解方法， 下一篇介绍具体程序实现。

在深入程序的实现之前，首先说明一下游戏的求解思路：

游戏求解是基于数字提示的约束， 每一行、列的可能状态是有限的。

有一种人类玩家的求解技术simple boxes， 可以确定一定被填色的格子：

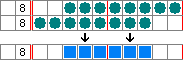
另一个例子：

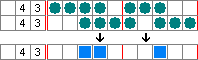
从最左到最右的填色方式中，均被填色的格子可以确定为填色格。

而要转化为程序求解技术， 需要记录在当前提示下可能的每种状态， 再对重合的状态进行确认。

标记单元格

为了方便说明， 首先仅考虑单行长度为10的一个例子：

最左：3 4 ⬛⬛⬛⬜⬛⬛⬛⬛⬜⬜

最右：3 4 ⬜⬜⬛⬛⬛⬜⬛⬛⬛⬛

中间：3 4 ⬜⬛⬛⬛⬜⬛⬛⬛⬛⬜

事实上， 由于3， 4的约束，黑格和白格共有五种可能状态：

• 第一组黑格之前的空格
• 第一组黑格
• 两组黑格之间的白格
• 第二组黑格
• 第二组黑格之后的白格

对格子作如下标记：

对于黑格， 按顺序递增标记， 对于空格， 由于空格长度可变， 用连续相同负数标记。

⬛⬛⬛⬜⬛⬛⬛⬛⬜⬜

2 ，3 ， 4， -5， 6，7，8，9，-10，-10

⬜⬜⬛⬛⬛⬜⬛⬛⬛⬛

-1， -1，2，3，4，-5， 6，7，8，9

⬜⬛⬛⬛⬜⬛⬛⬛⬛⬜

-1， 2， 3， 4， -5， 6， 7， 8， 9， -10

⬛⬛⬛⬜⬜⬛⬛⬛⬛⬜

2， 3， 4， -5，-5， 6， 7， 8， 9， -10

标记之后可以看到， 不论位置如何变化， 第二组第一个黑格的标记一定是6， 两组黑格之间的白格标记一定是-5。

得到单元格标记集

于是， 就可以通过上述标记来得到每个格子可能的标记，确定黑格，还是以单行为例，步骤如下：

• 对于所给提示 3 4 生成标记序列-1， 2， 3， 4， -5， 6， 7， 8， 9， -10（空格标记相同， 只需要记录一个）
• 找到最左，最右情况下每个单元格的标记（对应上面的第一种， 第二种标记）
• 可见第一个单元格的标记在最左情况下为2， 最右情况为-1， 得到第一个单元格的可能标记集合为标记序列中-1和2之间的所有标记， 在这个例子中只有{-1， 2}，表示第一个单元格可能是第一组黑格之前的空格， 也可能是第一组第一个黑格，每个单元格以此类推。
• 对于每个单元格， 如果标记集合只含正数或只含负数， 则可以确定状态。如第三格集合为{2， 3， 4}都是正数， 那么一定是黑格。

进一步求解

通过这种标记方式就得到了单行提示所能确定的格子， 下一步还需要融合行列的求解结果， 进一步求解。要进一步求解， 就需要在某个格子被填黑后更新整行的标记集合。还是以上面的例子， 假设在列求解中，这一行的第一格被填黑，那么显然应该可以得到第一组黑格一定是前三个格子。

3 4⬛⬛⬛⬜…

这个过程可以通过标记之间的映射来完成。

前三格在上述过程中得到的标记集分别为{-1，2}，{-1， 2， 3}，{2， 3， 4}， 在第一格被填黑后， 去除第一格的负标记，变为{2}， 由标记序列可以知道， 2之后的标记一定是3， 即确定第二格标记集{3}， 3之后一定是4， 第三格标记集变为{4}。

这个向前传播的过程需要每个标记之后可能出现的标记， 注意对于负数， 空白格之后可能再出现空白格，所以负数重复两次， 3 4标记序列变为：

[-1， -1，2，3，4，-5，-5，6，7，8，9，-10，-10]

对这个序列位移-1得到：

[ -1，2，3，4，-5，-5，6，7，8，9，-10，-10]

二者对应， 得到映射-1->(-1,2)，2->3, 3->4, 4->-5, -5->(-5, 6), 6->7 …..

即得到了每个标签之后可能出现的标签。

反之， 进行+1位移后可以得到每个标签前可能出现的标签， 进行反向传播。

求解过程

有了上述的求解方法， 就可以进行实际求解了。求解之前初始化，即生成每一行，每一列的标记序列和单元格标记集合，即每一个单元格分别有行和列提示生成的标记集合。

求解分为三个步骤：

• 确认棋盘格状态，即填色全正/全负标记的单元格
• 根据单元格填色更新标签集（某个单元格可能列集合全正被填色， 需要去掉行集合负标记）
• 进行前向/反向传播

不断循环这三个步骤，直至不再有新的格子被填色。

至此，对于解唯一的游戏，这个求解器已经可以得到解了，求解50*50的游戏用时约 0.5 s。

下面为一个小例子：

Enter board size:
10 5
Enter row hint:
2
2,1
1,1
3
1,1
1,1
2
1,1
1,2
2
Enter col hint:
2,1
2,1,3
7
1,3
2,1
deterministic solve completed in 8ms
solution:01100011010010101110101001010000110010100101111000
⬜⬛⬛⬜⬜
⬜⬛⬛⬜⬛
⬜⬜⬛⬜⬛
⬜⬛⬛⬛⬜
⬛⬜⬛⬜⬜
⬛⬜⬛⬜⬜
⬜⬜⬛⬛⬜
⬜⬛⬜⬛⬜
⬜⬛⬜⬛⬛
⬛⬛⬜⬜⬜

DFS

而对于解不唯一的游戏， 一定有单元格还有多个标签， 需要对这些格子的状态进行猜测。可以直接dfs确定一个未确定格子的状态， 再用求解器求解。伪代码如下:

void dfs(){
    if(visitedBoard){
        return;
    } else {
        mark board as visited; // use hash
    }
    if(game solved)return;
    for (cell: board){ // iterate through board cells
        if(cell has multiple label){
            record = current state; // record current board and labels
            cell_label = select(labels); // select one label
            solve(); // use solver
            dfs();
            state = record; //recover state
        }
    }
}

加上dfs后， 就可以得到多个解了。

如每行每列提示均为1 1的4*4游戏：

See also

• Nonogram Solver 2